divendres, 30 de gener del 2009
Exercici 10: Color
Exemple de dibuix pintat amb ... 
colors clars:
colors clars i foscos:
colors foscos:
colors clars: colors clars i foscos:Exercici 9: Il·lustració
Text:
"En comptes de cabells, li naixia una mata espessa de molsa, i a la cara coroneta tenia un niu d'aloses amb dos pollets. La mare voletejava entorn del seu cap. A la cara li creixia una barba d'herba diminuta plena de petites margarides que semblaven agulles de cap"
Il·lustració d'exemple per aquest text:
Il·lustració d'exemple per aquest text:
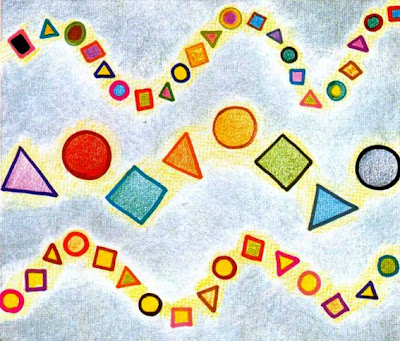
Exercici 8: Ritmes
Per aconseguir un ritme altern, podem canviar alternativament la forma, la mida i el color de les figures. Aquest tipus de ritme permet fer moltes combinacions diferents. A continuació en pots veure 2 exemples:
El quadrat
El quadrat és una figura geomètrica plana de quatre costats. També s'anomena quadrilàter regular perquè té els costats iguals i els angles rectes.
El traçat geomètric d'un quadrat es pot fer de 2 maneres diferents:
1. Traçat d'un quadrat donat un costat
· Dels extrems del costat AB tracem 2 perpendiculars amb l'ajuda de l'escaire i el cartabó. Les anomenarem L i M.
· Després traçarem 2 arcs amb centre a A i B i amb raci AB. Quan aquests arcs tallin les perpendiculars que hem dibuixat abans, trobarem els vèrtexs superiors C i D.
· Per completar el quadrat caldrà que acabem d'unir els punts A, B, C i D amb rectes.
2. Traçat d'un quadrat donat el radi de la circumferència circumscrita
· Dibuixem la circumferència amb el radi donat.
· Dibuixem el diàmetre AB i en perpendicular a aquest (utilitzar joc d'escaires) el diàmetre CD.
· Per últim unim els vèrtexs A, B, C i D, que són els extrems dels 2 diàmetres.
El traçat geomètric d'un quadrat es pot fer de 2 maneres diferents:
1. Traçat d'un quadrat donat un costat
· Dels extrems del costat AB tracem 2 perpendiculars amb l'ajuda de l'escaire i el cartabó. Les anomenarem L i M.· Després traçarem 2 arcs amb centre a A i B i amb raci AB. Quan aquests arcs tallin les perpendiculars que hem dibuixat abans, trobarem els vèrtexs superiors C i D.
· Per completar el quadrat caldrà que acabem d'unir els punts A, B, C i D amb rectes.
2. Traçat d'un quadrat donat el radi de la circumferència circumscrita
· Dibuixem la circumferència amb el radi donat.· Dibuixem el diàmetre AB i en perpendicular a aquest (utilitzar joc d'escaires) el diàmetre CD.
· Per últim unim els vèrtexs A, B, C i D, que són els extrems dels 2 diàmetres.
El triangle equilàter
El triangle és la figura geomètrica plana que té menys costats. El triangle regular s'anomena equilàter i té tres costats iguals i tres angles iguals.
El traçat geomètric d'un triangle equilàter es pot fer de dues maneres diferents:
1. Traçat a partir d'un costat del triangle equilàter
· Dibuixem el costat donat.
· Amb centre als extrems A i B tracem 2 arcs de radi igual a la mida del costat.
· El punt en què els arcs es tallen és el vèrtex C. Unint A, B i C amb el punt D obtenim el triangle equilàter.
El traçat geomètric d'un triangle equilàter es pot fer de dues maneres diferents:
1. Traçat a partir d'un costat del triangle equilàter
· Dibuixem el costat donat.· Amb centre als extrems A i B tracem 2 arcs de radi igual a la mida del costat.
· El punt en què els arcs es tallen és el vèrtex C. Unint A, B i C amb el punt D obtenim el triangle equilàter.
2. Traçat a partir del radi de la circumferència on està inscrit
· Dibuixem la circumferència partint del radi donat.
· Amb centre a l'extrem A d'un diàmetre AD, tracem un arc de radi AO.
· Unim els 2 punts amb què l'arc talla amb la circumferència B i C, i cadascún d'aquests amb D.
Subscriure's a:
Missatges (Atom)