divendres, 30 de gener del 2009
Exercici 10: Color
Exemple de dibuix pintat amb ... 
colors clars:
colors clars i foscos:
colors foscos:
colors clars: colors clars i foscos:Exercici 9: Il·lustració
Text:
"En comptes de cabells, li naixia una mata espessa de molsa, i a la cara coroneta tenia un niu d'aloses amb dos pollets. La mare voletejava entorn del seu cap. A la cara li creixia una barba d'herba diminuta plena de petites margarides que semblaven agulles de cap"
Il·lustració d'exemple per aquest text:
Il·lustració d'exemple per aquest text:
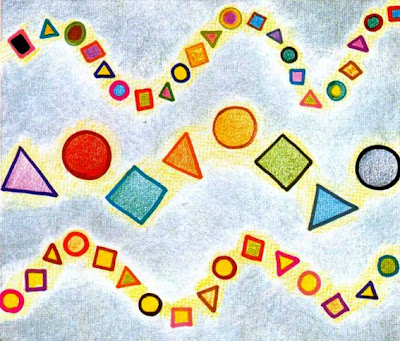
Exercici 8: Ritmes
Per aconseguir un ritme altern, podem canviar alternativament la forma, la mida i el color de les figures. Aquest tipus de ritme permet fer moltes combinacions diferents. A continuació en pots veure 2 exemples:
El quadrat
El quadrat és una figura geomètrica plana de quatre costats. També s'anomena quadrilàter regular perquè té els costats iguals i els angles rectes.
El traçat geomètric d'un quadrat es pot fer de 2 maneres diferents:
1. Traçat d'un quadrat donat un costat
· Dels extrems del costat AB tracem 2 perpendiculars amb l'ajuda de l'escaire i el cartabó. Les anomenarem L i M.
· Després traçarem 2 arcs amb centre a A i B i amb raci AB. Quan aquests arcs tallin les perpendiculars que hem dibuixat abans, trobarem els vèrtexs superiors C i D.
· Per completar el quadrat caldrà que acabem d'unir els punts A, B, C i D amb rectes.
2. Traçat d'un quadrat donat el radi de la circumferència circumscrita
· Dibuixem la circumferència amb el radi donat.
· Dibuixem el diàmetre AB i en perpendicular a aquest (utilitzar joc d'escaires) el diàmetre CD.
· Per últim unim els vèrtexs A, B, C i D, que són els extrems dels 2 diàmetres.
El traçat geomètric d'un quadrat es pot fer de 2 maneres diferents:
1. Traçat d'un quadrat donat un costat
· Dels extrems del costat AB tracem 2 perpendiculars amb l'ajuda de l'escaire i el cartabó. Les anomenarem L i M.· Després traçarem 2 arcs amb centre a A i B i amb raci AB. Quan aquests arcs tallin les perpendiculars que hem dibuixat abans, trobarem els vèrtexs superiors C i D.
· Per completar el quadrat caldrà que acabem d'unir els punts A, B, C i D amb rectes.
2. Traçat d'un quadrat donat el radi de la circumferència circumscrita
· Dibuixem la circumferència amb el radi donat.· Dibuixem el diàmetre AB i en perpendicular a aquest (utilitzar joc d'escaires) el diàmetre CD.
· Per últim unim els vèrtexs A, B, C i D, que són els extrems dels 2 diàmetres.
El triangle equilàter
El triangle és la figura geomètrica plana que té menys costats. El triangle regular s'anomena equilàter i té tres costats iguals i tres angles iguals.
El traçat geomètric d'un triangle equilàter es pot fer de dues maneres diferents:
1. Traçat a partir d'un costat del triangle equilàter
· Dibuixem el costat donat.
· Amb centre als extrems A i B tracem 2 arcs de radi igual a la mida del costat.
· El punt en què els arcs es tallen és el vèrtex C. Unint A, B i C amb el punt D obtenim el triangle equilàter.
El traçat geomètric d'un triangle equilàter es pot fer de dues maneres diferents:
1. Traçat a partir d'un costat del triangle equilàter
· Dibuixem el costat donat.· Amb centre als extrems A i B tracem 2 arcs de radi igual a la mida del costat.
· El punt en què els arcs es tallen és el vèrtex C. Unint A, B i C amb el punt D obtenim el triangle equilàter.
2. Traçat a partir del radi de la circumferència on està inscrit
· Dibuixem la circumferència partint del radi donat.
· Amb centre a l'extrem A d'un diàmetre AD, tracem un arc de radi AO.
· Unim els 2 punts amb què l'arc talla amb la circumferència B i C, i cadascún d'aquests amb D.
Traçat de rectes paral·leles i perpendiculars amb l'escaire i el cartabó
Per utilitzar bé l'escaire i el cartabó haurem de fer diverses proves i aprendre els diferents tipus de traçat que permeten de fer. Les 2 imatges següents mostren com col·locar-los per dibuixar rectes paral·leles (1ª imatge) i rectes perpendiculars (2ª imatge).
Els plans
Qualsevol superfície de dues dimensions (altura i amplada) és un pla.
Si mires el teu voltant veuràs plans de mides, colors i formes diferents. El contorn dels plans es pot descriure amb una línia que en marca els límits i la forma.
Les superfídies dels plans poden ser satinades, rugoses, aspres, suaus, granulades, etc.
Els tipus de plans
Els plans poden ser geomètrics o orgànics.
Si mires el teu voltant veuràs plans de mides, colors i formes diferents. El contorn dels plans es pot descriure amb una línia que en marca els límits i la forma.
Les superfídies dels plans poden ser satinades, rugoses, aspres, suaus, granulades, etc.
Els tipus de plans
Els plans poden ser geomètrics o orgànics.
Les línies
Si damunt d'un paper fas pressió amb un llapis, el senyal que hi deixa és un punt. Si a partir d'aquest punt mous el llapis en qualsevol direcció, el resultat és una línia.
La pressió, la manera com col·loquem el llapis i el recorregut que fem determinaran la línia que sorgirà. El tipus de línia també canviarà segons el paper, el llapis, el pinzell, el bolígraf ..., que utilitzem.
La pressió, la manera com col·loquem el llapis i el recorregut que fem determinaran la línia que sorgirà. El tipus de línia també canviarà segons el paper, el llapis, el pinzell, el bolígraf ..., que utilitzem.
La representació de les formes
A l'hora de representar les formes podem destacar aspectes diferents, segons el nostre estil i el nostre gust, segons el missatge que vulguem comunicar o segons la funció que hagi de fer el dibuix.
A continuació veurem 3 maneres de representar les formes.
El contorn exterior
És la línia que envolta el perfil de les figures. Dibuixem una forma per mitjà del contorn exterior quan hem d'expressar una idea de manera clara, concisa i sense detalls.
Són les línies, els colors i les textures que configuren l'interiro d'una forma. Dibuixem una forma per mitjà del contorn interior quan volem descriure-la detalladament.
És la representació d'una figura mitjançant un sol color sobre un fons diferent. En aquest cas, el contorn interior i l'exterior desapareixen i sorgeix un color pla. Dibuixem una silueta quan volem destacar una figura o quan volem imitar un efecte de contrallum.
A continuació veurem 3 maneres de representar les formes.
El contorn exterior
És la línia que envolta el perfil de les figures. Dibuixem una forma per mitjà del contorn exterior quan hem d'expressar una idea de manera clara, concisa i sense detalls. El contorn interior
Són les línies, els colors i les textures que configuren l'interiro d'una forma. Dibuixem una forma per mitjà del contorn interior quan volem descriure-la detalladament. La silueta
És la representació d'una figura mitjançant un sol color sobre un fons diferent. En aquest cas, el contorn interior i l'exterior desapareixen i sorgeix un color pla. Dibuixem una silueta quan volem destacar una figura o quan volem imitar un efecte de contrallum.dimarts, 27 de gener del 2009
Subscriure's a:
Missatges (Atom)